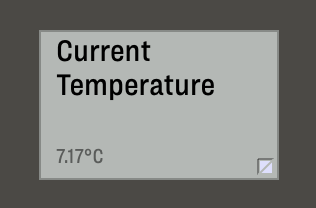
How about a note with the current outside temperature?
Using https://openweathermap.org:
$URL = https://api.openweathermap.org/data/2.5/weather?id=6947478&appid={yourAppId}&units=metric
“yourAppId” is the API key you get for free after registering with openweathermap.org.
$AutoFetchCommand = if($Text.contains(“.temp.:([0-9.]+)”)){ $Temperatur = $1; };
you will get:
Weather.tbx (81.2 KB)